Applications of Convolution in life
Definition of convolution
In mathematics, convolution is a mathematical operation on two functions (\(f\) and \(g\)) that produces a third function (\(f*g\)) that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reversed and shifted. The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, it differs from cross-correlation (\(f*g\))only in that either \(f(x)\) or \(g(x)\) is reflected about the y-axis; thus it is a cross-correlation of \(\ f(x)\) and \(g( - x)\), or \(f( - x)\) and \(g(x)\). For complex-valued functions, the cross-correlation operator is the adjoint of the convolution operator.
Convolution has applications that include probability, statistics, acoustics, spectroscopy, signal processing and image processing, geophysics, engineering, physics, computer vision and differential equations.
Applications of convolution
Image Processing
Image processing in spatial domain is a visually rich area of study dealing with pixel-manipulation techniques. Different operations are performed over the images, which are treated simply as two-dimensional arrays.
Normally, all these matrix-based operations are performed between a larger matrix (representing the complete image) and a smaller matrix (which is known as a 2D kernel). The kernel size and the associated values determine the impact exerted by it on the image considered.
For example, suppose we have a matrix [0 1;-1 0] and convolve it an image as seen in Figure 1(a); the result will be like the one shown in Figure 1(b). We can see that the convolving operation has led to the determination of edges prevalent in the figure. However, the result obtained is incomplete because we don't yet have the complete set of edges.
In order to get the remaining set of edges, we need to perform the convolution operation once more. But this time our kernel will be [0 -1;1 0] instead of [0 1; -1 0]. The edges resulting from this are as shown in Figure 1(c).
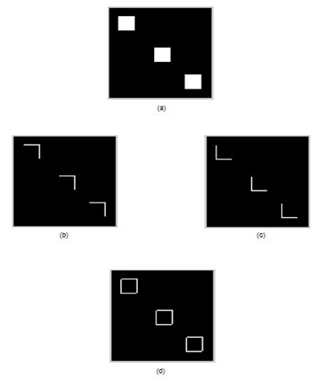
Following this, we need to combine the results of both operations above to attain all of the edges present in the image (Figure 1(d)). The pair of kernels mentioned are named as Roberts' kernels and the entire act performed on the original image is known as Roberts' edge detection.
Audio Processing
Auditoriums, cinema halls, and other similar constructions heavily rely on the concept of reverberation because it enhances the quality of sound greatly.
The process in which reverberation is digitally simulated is technically termed "convolution reverb". With convolution reverb, you can convolve an area's known impulse response with that of a desired sound in order to simulate the reverberation effect of a particular area.
Convolution reverb uses digital recordings of physical spaces or other reverb effects (impulse responses) to recreate their reverb. Convolution reverb is often used in film production, with sound engineers recording impulse responses of sets and locations so sounds can be added in post-production with realistic reverberation.
One great example of this is in the movie A Star Is Born, where the band recorded live between sets at Coachella and other festivals but played un-amplified to the crowd. The production team took impulse responses of the full sound system in the crowd to emulate what the band would've sounded like if they were amplified, which gave the live performances a live and very authentic feel.

Optics Processing
When collimated light passes through an aperture with a slit in it, the light gets diffracted along the discontinuity. This act results in the formation of a sinc function on the plane placed at infinity which is referred to as the diffraction pattern of light passing through the slit. Likewise, for a circular aperture, the resulting diffraction pattern would be a sombrero function (Introduction to Imaging Spectrometers).
Now, suppose that we have an aperture which is a combination of both of these (slits and circular shapes). we can arrive at the diffraction pattern of this complex structure without actually repeating the process. In fact, the resulting pattern will be the pattern obtained by convoluting the sinc function with that of sombrero.
This indicates that, when we know the diffraction patterns for each kind of aperture, the diffraction pattern of a combination of them can be obtained by convolving these individual patterns. A similar kind of superposition-like behavior is exhibited by most of the linear systems that convolution can help simplify.
Conclusion
This article discusses the applications of some convolution operations in daily life. We can find convolution and related operations in many applications of science, engineering, and mathematics. So it's very important to learn convolution.